Դեկտեմբերի 22

77.40, 15,
78. 39 13
79.20
80.49
81 56
82 27
Միջին դպրոց 9-4 դասարան
Դեկտեմբերի 22

77.40, 15,
78. 39 13
79.20
80.49
81 56
82 27
Դասարանում

69.=135+12+35=180:2=90
90-12=78
90-35=55
70.340+80=420:3=140
140×5=560+340=900
140տետր
ը
900փողը
71.1+4=5
105:5=21
21×2=42
105-42=63
72.=5+8+11=24
312:24=13
13×5=65
13×8=104
13×11=141
Տանը

73.186:3=62
62+8=70
62-8+3=57
62+70+57=186
74.84-4-5-9=66:3=22
22+4=26
22+9=31
22+5=27
75
416:2=208
1) Աստղանիշի փոխարեն տեղադրե՛ք > կամ < նշաններից որևէ մեկն
այնպես, որ ստացվի ճիշտ անհավասարություն.
ա) 5 · 7 > –1,
բ) 0 < (–3) · (–4),
գ) (–1) · (–4) > –1,
դ) –4 < 2 · 3,
ե) (–5) · 2 > 0,
զ) 5 · 7 < (–4) · (–9)։
2) Կատարե՛ք գործողությունները.
ա) (–2) · (|–4| – |–8|), =8
բ) (|–21|+|+4|) ։ (–5),=-5
գ) ((–3) · (–7) – (–2) · |–4|) · (–6), =-78
դ) (|–9|+|–1|) ։ (18–(–|6|))։=10/12
3) Ո՞ր թվանշանով է վերջանում 5-ի բաժանվող զույգ թիվը։
0 վերգով
4)120-ը 480-ի քանի տոկոսն է։
25%
Լրացուցիչ(տանը)
5) Տրված է երկու կոտորակ։ Առաջին կոտորակի համարիչը 6 անգամ
մեծ է երկրորդ կոտորակի համարիչից, իսկ հայտարարը 5 անգամ
փոքր է երկրորդ կոտորակի հայտարարից։ Ինչի՞ է հավասար
առաջին և երկրորդ կոտորակների հարաբերությունը։
6/5:1/25
6) Թվի կեսի կեսը հավասար է 12-ի։ Գտե՛ք այդ թիվը։
12×4=48
7) Առաջին փականագործին 120 մանրակ պատրաստելու համար
պետք է 3 ժամ, իսկ երկրորդին՝ երկու անգամ ավելի։ Ինչքա՞ն
ժամանակում փականագործները, աշխատելով միասին, կպատրաստեն 600 մանրակ։
120:3=40×2=80
80+40=120
600:120=5
Առաջադրանքներ(դասարանում)
1) Գրե՛ք երեք հաջորդական ամբողջ թվեր, որոնց գումարը հավասար
է 0-ի։
-1+0+1=0
2) Հաշվել.
ա)( -44:4+12:(-3))-134=-149
բ) -12+(-34)-(-21)=25
գ) -34+6-91=-119
դ) -(-56)-(-21)+100=177
ե)-120:2+60=0
3) AB հատվածը C կետով բաժանվում է AC և CB երկու հատվածների։
CB հատվածի երկարությունը AC հատվածի երկարության 2/3-ն է։
Գտե՛ք AB հատվածի երկարությունը, եթե CB հատվածի երկարությունը 24 սմ է։
24:2×3+24=60
4) Արույրը 60 % պղնձի և 40 % ցինկի համաձուլվածք է։ Արույր պատրաստելու համար վառարանի մեջ դրել են ցինկ և 210 կգ պղինձ։
Որքա՞ն ցինկ են դրել վառարանի մեջ։ Որքա՞ն արույր կստացվի։
210+140=350 ,210×40:60=140
Լրացուցիչ(տանը)
5) Գտե՛ք արտահայտության արժեքը.
ա) (35 – 17) – 20=8, դ) (29 – 64) + 23=-12, է) (–39 –21) + 11=-7,
բ) (–43 – 14) – 32=3, ե) (–30 – 21) + 56=47, ը) (16 – 33) – 50=33,
գ) (–74 + 27) – 15=-32, զ) (81 – 45) – 60=-24, թ) (–18 + 6) – 39=27:
6) Հաշվե՛ք.
ա) | – 4 – *|,=1 եթե աստղանիշի փոխարեն գրված լինի –3 թիվը,
բ) |5 – * – 8|=4, եթե աստղանիշի փոխարեն գրվի –9 թիվը,
գ) |* – 2| + |* – (–1)|=9, եթե աստղանիշի փոխարեն գրվի 6 թիվը։
7) Քաղաքից դուրս եկավ մի մեքենա, որի արագությունը 80 կմ/ժ էր։
հետո նրա հետևից շարժվեց մեկ ուրիշ մեքենա, որի արագությունը
90 կմ/ժ էր։ Քաղաքից դուրս գալուց ինչքա՞ն ժամանակ անց
երկրորդ մեքենան առաջինից 20 կմ առաջ անցած կլինի։
2ժ
8) Գտնել բաց թողած թիվը.
Առաջադրանքներ(դասարանում)
1) Կոորդինատային ուղղի վրա պատկերեք A(-2) և B(3) կետերը: Գտնել A և B կետերի հեռավորությունը:
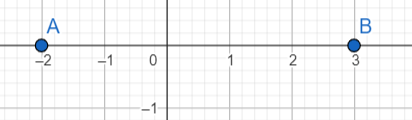
և իրենց հեռավորությունը 5
2) A կետի կոորդինատը –4 է։ Նրա ո՞ր կողմում է գտնվում և նրանից
քանի՞ միավոր հեռավորություն ունի B կետը, եթե վերջինիս
կոորդինատն է՝
ա) –8, բ) 1, գ) +6, դ) -10։

A B=4 A C=5 A D=10 A E=6
3) Գծե՛ք կոորդինատային ուղիղ և նրա վրա նշե՛ք A (–3), B (+7), C(–6), D (+1), E (+8), F (–5), G (–4) կետերը:

4) Կոորդինատային ուղղի վրա նշե՛ք –7, –5, –2, 0, +1, +4, +8, +10
թվերին համապատասխանող կետերը։

Լրացուցիչ(տանը)
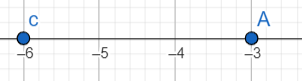
5)Կոորդինատային ուղղի վրա A (–6), B (+2), C (–3), D (–4), E (+8),
F (–2), G (–10) կետերից ո՞րն է գտնվում ամենից ձախ, և ո՞րը՝ ամենից
աջ։

ամենա աջը=E ամենա ձախը =G
6) Գծե՛ք կոորդինատային ուղիղ և նրա վրա նշե՛ք A (–3) կետը։ Նշե՛ք
նաև՝
ա) B կետը, որը գտնվում է A կետից երկու միավոր դեպի աջ,
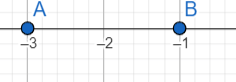
բ) C կետը, որը գտնվում է A կետից երեք միավոր դեպի ձախ։
7) Կոորդինատային ուղղի վրա քանի՞ բնական թիվ է գտնվում
հետևյալ թվերի միջև.
ա) –6 և 2=1, բ) 0 և 5=4, գ) -7 և 7=6:

8)* Գտնել բաց թողած թիվը.
13
Դասարանում

1=12կգ 18
2=6
3=40kg
4=25
5=80g

6=12
7=250×30=7500:1000=7,5
8=32×1000=32000+80=32080
9100:15×153=12000
10=100-34
8․A քաղաքից միևնույն ուղղությամբ դուրս եկան երկու ավտոմեքենա։ 8 ժամ հետո որքա՞ն կլինի նրանց միջև եղած հեռավորությունը, եթե առաջին ավտոմեքենան ժամում անցնում է 60կմ, իսկ երկրորդը՝ 80 կմ։
160
9․ Գնացքը 2 օրում միևնույն արագությամբ անցավ 1620կմ ճանապարհ։ Առաջին օրը նա ճանապարհի վրա ծախսեց 10 ժամ, իսկ երկրորդ օրը՝ 2 ժամ պակաս։ Որքա՞ն ճանապարհ նա անցավ առաջին օրը։
900կմ
10. 70% արծաթ պարունակող արծաթի և ոսկու համաձուլվածքում արծաթը 16կգ-ով ավելի է քան ոսկին։Քանի՞ գրամ ոսկի է պարումակում համաձուլվածքը:
1/1
12
1)Տրված են –5, –11, +18, –9, +6 թվերը։ Գտե՛ք՝
ա) այդ թվերի գումարին հակադիր թիվը,
+1
բ) այդ թվերին հակադիր թվերի գումարը։
1
2) Կոորդինատային ուղղի վրա նշե՛ք
A (–2), B (+5), C (–8), D (–1), E (+2) կետերը։

3) Գնացքը 3 ժամում անցավ 250 կմ։ Առաջին
ժամում այն անցավ ճանապարհի 40 %-ը,
երկրորդ ժամում՝ մնացածի 40 %-ը։ Քանի՞
կիլոմետր անցավ գնացքը երրորդ ժամում։
250:100×40=100
250-100=150
150:100×40=60
150-60=90
4)Կառքի առջևի անիվը 96 պտույտ է կատարում, երբ հետևի անիվը
կատարում է 64 պտույտ: Որքա՞ն է հետևի անիվի շրջագծի երկարությունը,
եթե առջևի անիվինը 2 մ է:
96:64=1,5
1,5×2=3
Լրացուցիչ(տանը)
5)Որո՞նք են այն չորս հաջորդական ամբողջ թվերը, որոնցից
ամենամեծը հավասար է՝ ա) –11-ի, բ) 0-ի, գ) +2-ի, դ) –1-ի։
a=-11, -12, -13,-14, b=0, -1 -2 -3 g= 2,1 0 -1 d=-1 -2 -3 -4
6)Ավտոբուսի արագությունը մեքենայի արագության 5/7-ն է։ Ինչքա՞ն է
մեքենայի արագությունը, եթե ավտոբուսի արագությունը նրանից
փոքր է 30 կմ/ժ-ով։
7/7-5/7=2/7
2/7X=30
x= 105
7)Ճի՞շտ է արդյոք, որ եթե
a + |a| = 0
գրառման մեջ a-ի փոխարեն գրենք որևէ բացասական թիվ, կստացվի
հավասարություն: Իսկ եթե գրենք զրո կամ դրակա՞ն թիվ:
այո:
0 -այո
դրական թիվ -ոչ
8)Գնել են երկու տեսակի կոնֆետներ` վճարելով ընդամենը
6500 դրամ: Առաջին տեսակի կոնֆետից, որի 1 կիլոգրամն արժե
2200 դրամ, գնել են 2 կգ: Մնացած գումարով գնել են երկրորդ
տեսակի կոնֆետներ` 1 կիլոգրամը 700 դրամով: Երկրորդ տեսակի
քանի՞ կիլոգրամ կոնֆետ են գնել: 2200×2=4400 6500-4400=2100 2100:700=3
Առաջադրանքներ(դասարանում)
Առաջադրանքներ(դասարանում)
1) Հաշվե՛ք.
ա) (–7) · (+16), =-112
բ) (+16) · (–4), =-64
գ) (–1) · (+1), =-1
դ) (+20) · (–19),=-380
ե) (–4) · (+5), =-20
զ) (+23) · (–6)=-138
2) Հաշվե՛ք.
ա) +38 ։ (–19)=-2
դ) –420 ։ (–15) =28
է) 0 ։ (–14)=0
բ) –600 ։ (–150)=4
ե) –531 ։ (+3) =-177
ը) –121 ։ (–11)=11
3) Գտե՛ք այն թիվը, որը աստղանիշի փոխարեն գրելու դեպքում
կստացվի հավասարություն.
ա) –3 · (-7)= 21,
գ) –10 · 0 = 0,
ե) –15 · (-3) = 45,
բ) 6 · (-6) = –36,
դ) –9 · 9 + 1 = –80,
զ) 3 · 7 = 21։
Լրացուցիչ(տանը)
4) Հաշվե՛ք.
ա) 8 ։ (–2) – 14 ։ (–7) + (–12) ։ 4,= -5 դ) (–55 ։ 11 + 48 ։ (–16)) ։ (–4)=2,
բ) –18 ։ (–9) + 16 ։ (–8) – 24 ։ (–6)=4, ե) –66 ։ (72 ։ (–9) + 105 ։ (–35))=6
գ) (33 ։ (–3) – 40 ։ (–8)) ։ (–3),=2 զ) –84 ։ (–56 ։ (–7) + 54 ։ (–9))=-42։
5) a-ի և b-ի ի՞նչ արժեքների դեպքում կստացվի հավասարություն.
ա) a : b = 0, a =0 , b=ցանկացած
գ) a : b = a, a -ցանկացած, b=1
ե) (–a) : b = –1, a=b
բ) a : b = 1, a=b
դ) a : b = –a, a- ցանկացած, b=-1
զ) a : (–b) = –1: a=b
6) Հայտնի են բաժանման հետևյալ հատկությունները.
(a + b) : c =,-6 ; (a + b) : c =-9
a : c + b : c,=-6 a : c + b : c,=-9
(a · b) : c=-40 (a · b) : c=54
(a : c) · b=-40; (a : c) · b=54
Ստուգե՛ք, որ այս հարաբերակցությունները ճիշտ են հետևյալ
ամբողջ թվերի համար.
ա) a = 20, b = 10, c = –5,
բ) a = –18, b = –9, c =3:
1) Հաշվե՛ք
ա) |– 6| + |-4|=10
բ) |– 50| + |+ 4|=54
գ) |– 18| · |– 21|=378
դ) |21| – |-6|=15
2) Առանց բազմապատկում կատարելու համեմատե՛ք.
ա) (–5) · (–21) > 0, դ) (+3) · (+9) > (+8) · (–7),
բ) (–8) · (+6) < 0, ե) (–14) · (–12) > (–10) · (-4),
գ) (+15) · (–4) < 0, զ) (+2) · (–1) < (–6) · (–31)։
3) Գտե՛ք արտահայտության արժեքը.
ա) (35 – 17) – 20,=-2 դ) (29 – 64) + 23=12
բ) (–43 – 14) – 32=9, ե) (–30 – 21) + 56=47:
գ) (–74 + 27) – 15=-32,
Լրացուցիչ(տանը)
4) Հաշվե՛ք
ա) |31| + |27|=58
բ) |44| : |– 4|=11
գ) |– 3| – |– 1|=2
դ) |15| · |– 12| =180
5) Գտե՛ք արտահայտության արժեքը.
ա) (79 – 45) – 60=-26, գ) (–18 + 6) – 30=18,
բ) (–33 –21) + 11,=-1 դ) (16 – 33) – 54=37:
6) Օգտվելով գումարման նկատմամբ բազմապատկման բաշխական
օրենքից՝ հաշվե՛ք հնարավորին չափ պարզ եղանակով.
ա) ( +5 ) · ( +3 ) + ( +5 ) · ( –2 )=5, գ) ( –7 ) · ( –4 ) + ( –7 ) · ( +3 )=7,
բ) ( –2 ) · ( +4 ) + ( –2 ) · ( –3 )=-2, դ) ( –6 ) · ( –5 ) + ( –6 ) · ( +4 )=6։
Լրացուցիչ

(1=6) 2=-8 3=-3 4=11 5=10 6= -4 7=3 8= -4 9=12 10=24 11=18 12=12 13=4 14=9 15=-5 16=-6 17=3 18=5 19=3 20=4